Recognize characteristics of graphs of polynomial functions
Polynomial functions of degree 2 or more have graphs that do not have sharp corners; recall that these types of graphs are called smooth curves. Polynomial functions also display graphs that have no breaks. Curves with no breaks are called continuous. Figure 1 shows a graph that represents a polynomial function and a graph that represents a function that is not a polynomial.
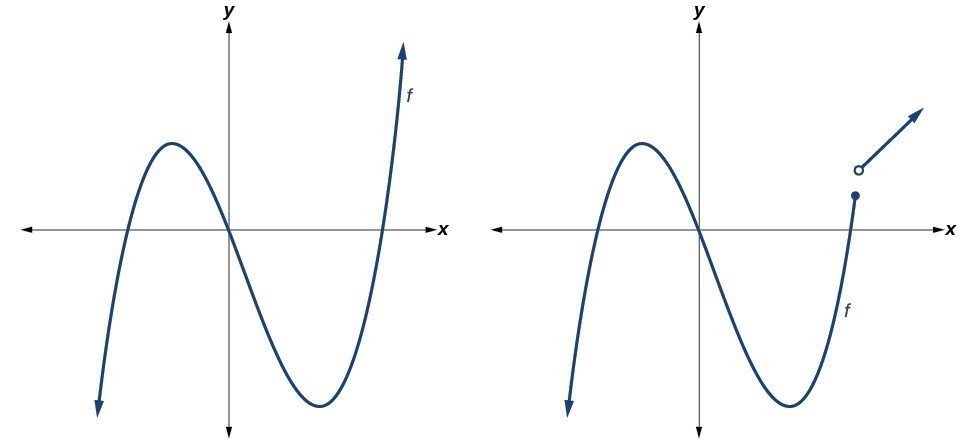 Figure 1
Figure 1Example 1: Recognizing Polynomial Functions
Which of the graphs in Figure 2 represents a polynomial function?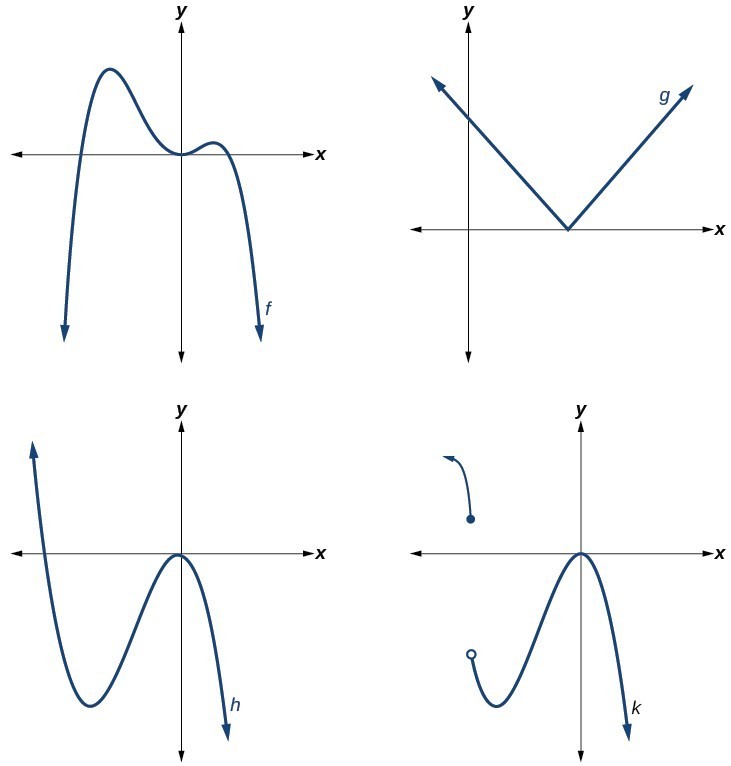 Figure 2
Figure 2Solution
The graphs of f and h are graphs of polynomial functions. They are smooth and continuous.
The graphs of g and k are graphs of functions that are not polynomials. The graph of function g has a sharp corner. The graph of function k is not continuous.
Q & A
Do all polynomial functions have as their domain all real numbers?
Yes. Any real number is a valid input for a polynomial function.
